Understanding Merkle Trees

I wrote this article in 2021 on Hashnode in a flurry of interest in cryptography. I am reposting it here to archive it.

In this article, we will build an understanding of Merkle Trees and their applications. What is a Merkle Tree? A Merkle Tree is a data structure that makes it efficient to verify the integrity of a collection of data. These data structures are used in all sorts of applications. Most notably, Merkle trees show up in peer-to-peer networks, blockchains, and version control systems.

Do you need to understand computer science and cryptography to understand Merkle Trees? No, but it might be helpful. As the applications of Merkle Trees have become more visible, there is more interest in how they work. Merkle Trees rely on cryptographic hash functions which rearrange bits to represent data. You can build your intuition about hash functions by reading Understanding SHA-1 with Python and learn some of the basics of how data is stored and transformed by computers by reading Binary and Hexadecimal and Cheatsheet: Bitwise Operators .

1. Applications

How are Merkle Trees used? The applications of Merkle Trees are broad, which is why they are incorporated in so many exciting projects. Merkle Trees allow us to ensure the integrity of data without doing large amounts of computation.

Merkle Trees are crucial for Peer-to-peer file exchange systems, where data is discovered and shared between computers, instead of being downloaded from a central server. Merkle trees allow a large collection of data (a database, document, video, etc.), to be broken up into blocks and downloaded block-by-block. Using a Merkle Tree, we download blocks from many different sources, and quickly check that the final data collection is exactly what we were expecting. If a single block of data is incorrect, we can efficiently identify this block, re-download it and check again if our updated dataset is correct.

Another way that Merkle Trees are used is in the verification of blockchain transactions. In their basic form, a blockchain is an immutable (unchangeable) record of transactions between parties. To make this record immutable, transactions must be verified by multiple parties which all come to a consensus about the “state” of the blockchain. Merkle Trees are crucial for Blockchains (including Bitcoin) to efficiently verify transactions. Because many different parties need to verify the presence of new transactions in a blockchain, it becomes infeasible for every party to verify every single transaction each time the blockchain state is updated. Instead of checking every transaction, Merkle Trees make it easy to perform a single check which validates the integrity of the entire history of transactions. At the end of this article, we will discuss how we can verify that certain data has been included in a Merkle Tree using a “Merkle Proof.”

One more widespread implementation of Merkle Trees is in Version Control systems like git. While this application may be less familiar to those without some experience in software development, version control is a crucial part of producing software collaboratively. Individual developers introduce changes to a software project, and version control systems track the time, lineage, and data of changes to the project (new lines of code, renamed files, deleted files, etc.). Merkle Trees allow changes to a software project to be recorded in an efficient format that can be quickly validated. Because of Merkle Trees, developers can agree on the state of a software project and incrementally introduce updates to that state, creating a “version history” of the project.

2. The fundamentals

So how do Merkle Trees work? Merkle Trees (also called hash trees) are built out of cryptographic hashes. A cryptographic hash function takes an arbitrary array of bits and maps it to a completely unique output.

As an example:

SHA1(“foo”) = “0beec7b5ea3f0fdbc95d0dd47f3c5bc275da8a33”

Our hash function here is called Secure Hashing Algorithm 1 (SHA-1) and our input is “foo.” The hash function returns 160 bits that are completely unique to the input “foo.” This is not very helpful for storing a single word, but it is crucial for verifying the integrity of large blocks of data. Instead of comparing two blocks of data which could have thousands (or millions) of bits, we can compare two 160 bit hashes that exactly identify the content of the data blocks. Obviously, this is much more efficient.

Note: because the output of a hash function is just an array of bits, we can get the hash of other hashes.

SHA1(“0beec7b5ea3f0fdbc95d0dd47f3c5bc275da8a33”) = “2865765152809a426f118f48c468c5f459425211”

This is precisely how Merkle Trees work. We build a tree of hashes, hashes of hashes, and hashes of hashes of hashes, etc.

Note: SHA-1 is deprecated because it has been demonstrated to produce the same hash for different inputs. We are using it here because it has a manageable digest size.

3. Building a Merkle Tree

Now that we have covered the fundamentals, we will build ourselves a simple Merkle Tree to show exactly how it is constructed step-by-step.

A Merkle Tree is called a “tree” because the data structure resembles a tree which goes from a “root” node to a collection of “leaf” nodes.

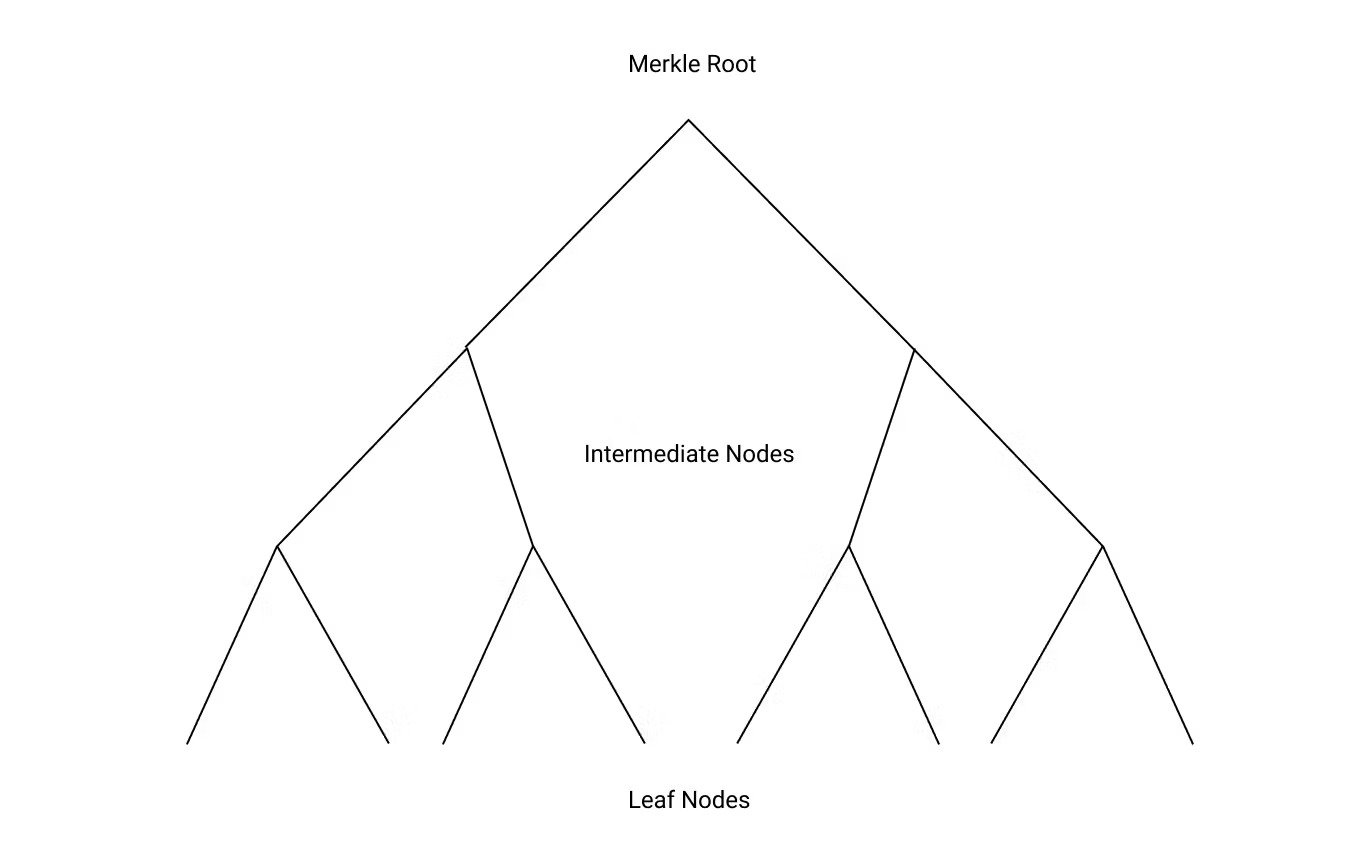
Fig 1.jpg

The leaf nodes of a Merkle Tree are constructed from hashes of data blocks. In the peer-to-peer network case this could be sections of a file, for a blockchain it would be individual transactions, and for a version control system it would be individual lines of code, for example.

Consider an example Merkle Tree with four blocks of data. (1) We build our tree by calculating the hashes of the data blocks first. These hashes make our “leaf nodes.” (2) We then concatenate adjacent leaf hashes together, and calculate their combined hash, forming our “intermediate” nodes. (3) Finally, we calculate the hash of the concatenated hashes of the of “intermediate” nodes. This final step produces our “root” hash. Note that the root hash contains information about every leaf node. If a single leaf node changes, the root hash will also change.

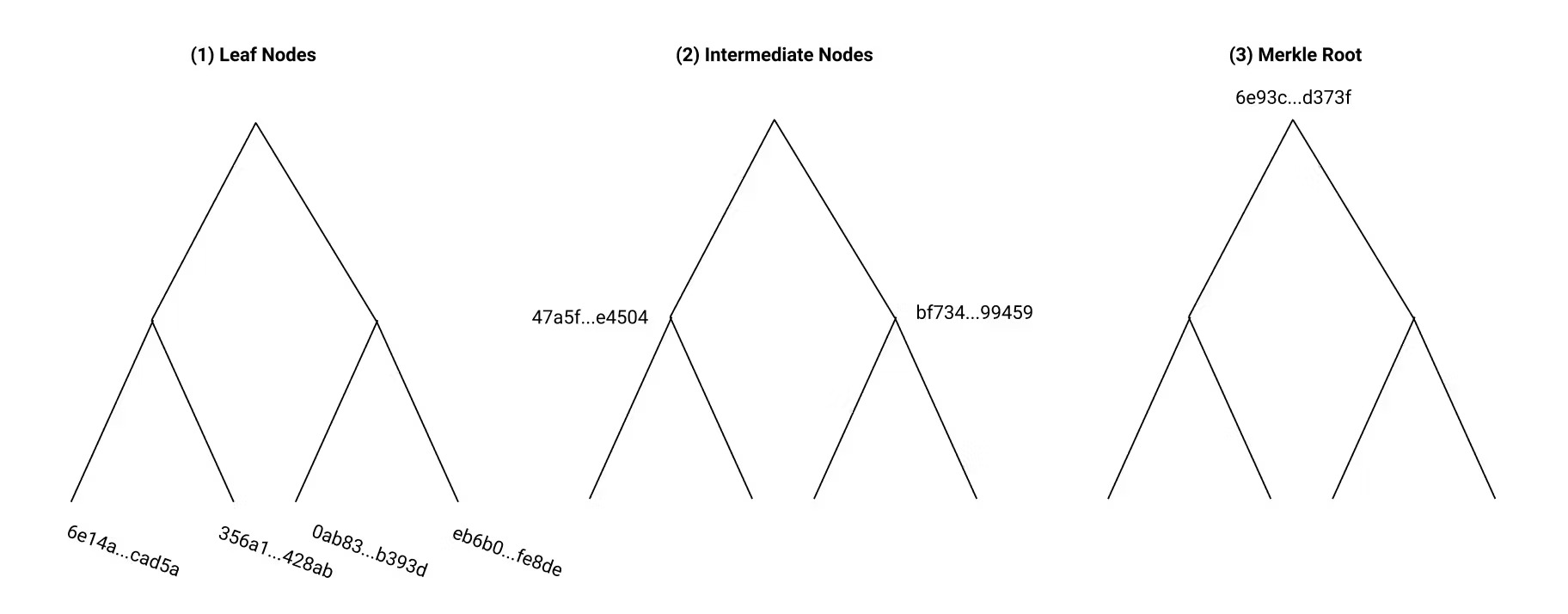
Fig 2.jpg

Two notes about Merkle Trees:

(1) We are using a simple example with 4 data blocks. In real life, our Merkle Tree could have hundreds or thousands of leaf nodes and therefore, many more intermediate nodes.

(2) Because we must use a binary tree, we may have to “balance” a tree if it has an uneven number of leaf nodes. We could do that by creating data blocks full of zeros as our final leaf node.

5. Using a merkle tree

So, now that we have put together a merkle tree, let’s look at how we can use it to verify the integrity of our data. As we noted above, a leaf node corresponds to a section of data, and if the data in a single leaf changes, this will also change the root hash of the entire Merkle Tree.

We will use the example of peer-to-peer networks. In these networks, data can be transferred from untrusted peers, and is validated with a trusted root hash. If we are downloading data in a peer-to-peer network, we retrieve the expected root hash, then download blocks of data from many different untrusted sources. We construct the final data collection according to a defined pattern, and calculate a Merkle Tree. We then check that the root hash of our Merkle Tree is the same as the root hash we were expecting.

The important piece of this process is what we do if we find that the root hash isn’t what we expected. In this case, we can efficiently identify a problem block and replace it. If we find that our root hash isn’t what we expected, we can go down a level in the tree. At this level, we find that one hash is what we expect and the other isn’t. For the hash that we expected, we don’t have to worry about any of the hashes at a lower level. Instead, we only look at the next level for the hashes that don’t agree. In this case, we can identify the problem block in the tree without checking the hashes of every leaf node. This is exactly what makes Merkle Trees efficient for verifying data integrity.

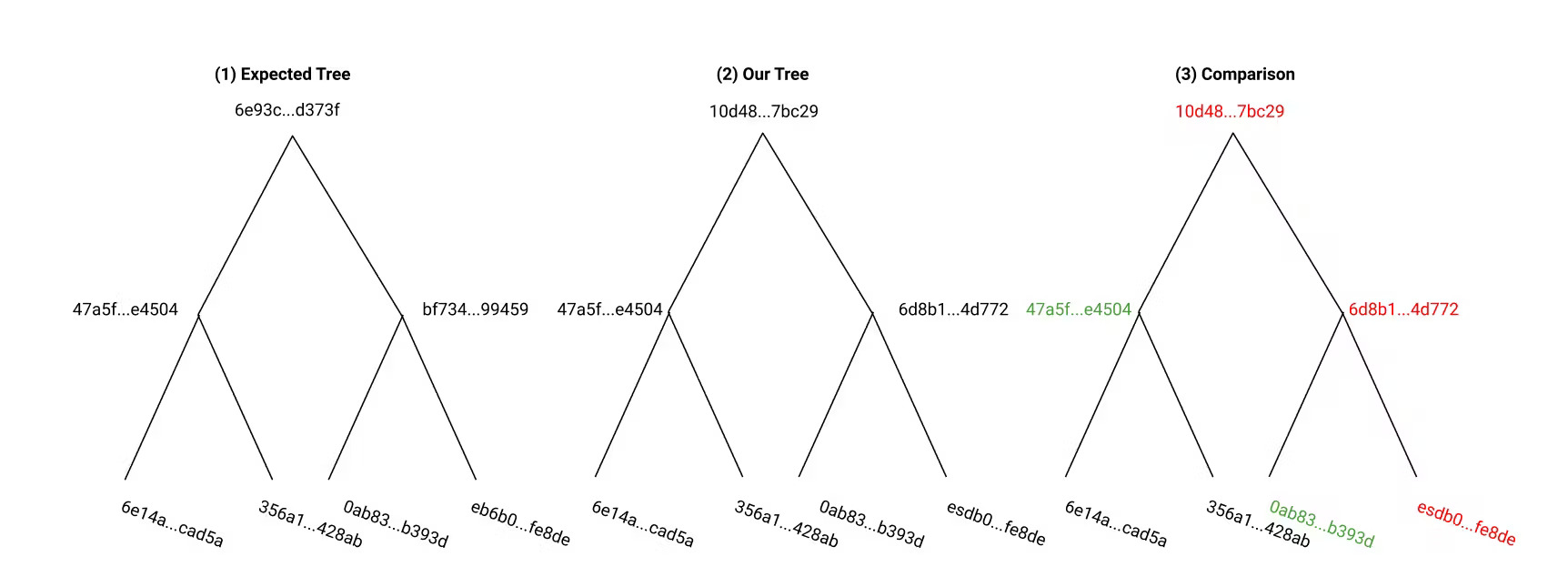
Fig 3.jpg

In fact, using a Merkle Tree means that we only need to compute log2(N) hashes where N is the number of leaf nodes.

6. A Merkle Proof

Another use of Merkle Trees is for parties to verify that a certain piece of data has been included in a given tree. We do this using a “Merkle Proof.” These proofs are most relevant to blockchains, where they are used to demonstrate that a certain transaction has been included in a “block.” The terminology is a bit confusing here. Above, we described leaf nodes corresponding to “blocks” of data. Here, a “block” is a collection of transactions, recorded as a Merkle Tree, hence the terminology “Block-chain.”

If I have a transaction (actually, the hash of a transaction) that I would like to verify, I can ask someone who has stored the entire transaction history of a blockchain (a “full node” in Bitcoin parlance) to prove to me that they have included the specific transaction I am interested in. I know:

The hash of my transaction.
The root hash of the entire block of transactions.

To verify that my transaction was included in a block, I request only the specific intermediate nodes in the tree structure that I need to complete my own version of the Merkle Tree, using my own version of the transaction hash. I can then “rebuild” the tree and recompute the root hash, to verify that my new root hash is the same as the root hash I was expecting. This “proves” to me that my transaction was included in the block. If it wasn’t, I would get a completely different root hash.

7. Conclusion

This is an overview of how Merkle Trees work, and an example of a few of their applications. Hopefully you are encouraged to play around with a Merkle Tree data structure and better appreciate the applications that implement them.